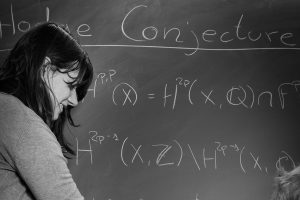Search
We go to the Faculty of Mathematics at the University of Valencia, where Isabel Cordero Carrión talks about her areas of research: applied mathematics and astrophysics, and her interest in gravitational waves.
Frederick Leung, Professor of Mathematics Education at the University of Hong Kong, investigates how socio-cultural circumstances affect mathematical ability.
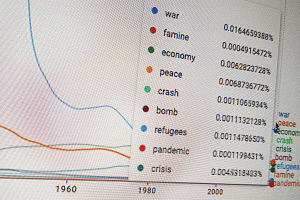
Recent advances in complex systems research, computer-based simulations, and large-scale databases, are paving the way towards fully developing a mathematical theory of human history.
Fractals are mathematical structures that come from a very simple equation, but have a little twist that makes them slightly more complicated, generating «self-similar» structures.
The Riemann hypothesis is an unproven statement referring to the zeros of the Riemann zeta function.
Mathematically, the motion of a fluid is described by the so-called Navier-Stokes equations. In the spirit of Newtonian mechanics, these equations should determine the future motion of the fluid out of its initial state.
The aim of this article is to highlight some previous challenges that were also a stimulus to finding proof for some interesting results. With this pretext, we present three moments in the history of mathematics that were important for the development of new lines of research.
The Hodge conjecture, proposed in 1950, is one of the seven millennium problems, and is framed within differential geometry and algebraic geometry.
The Poincaré conjecture is a topological problem established in 1904 by the French mathematician Henri Poincaré. It characterises three-dimensional spheres in a very simple way. This problem was directly solved between 2002 and 2003 by Grigori Perelman, and as a consequence of his demonstration of the Thurston geometrisation conjecture.
- 1
- 2