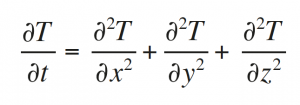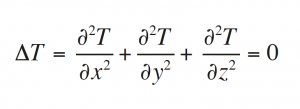The Hodge conjecture

The Hodge conjecture is one of the seven millennium problems, and is framed within differential geometry and algebraic geometry. It was proposed by William Hodge in 1950 and is currently a stimulus for the development of several theories based on geometry, analysis, and mathematical physics. It proposes a natural condition for the existence of complex submanifolds within a complex manifold. Manifolds are the spaces in which geometric objects can be considered. In complex manifolds, the structure of the space is based on complex numbers, instead of the most intuitive structure of geometry, based on real numbers.

Keywords: complex geometry, topology, homology, Hodge theory, manifolds.

Communicating mathematics

Mathematics has become a highly technical discipline, with many fields and subfields. The language of mathematical research is extremely abstract. For this reason, when mathematicians are confronted with the task of explaining a problem to the general public, they notice the chasm between what is currently understood as mathematics and the way researchers work. However, mathematicians recognise the importance of disseminating their most notable advances and of doing so using the most accessible language possible. This is why conferences with high media exposure are held, why honours are awarded to mathematicians who have made great advances, and prizes are offered for the solution of specific problems. The seven millennium problems are a good example. These are not problems for the average person. Instead, they direct work towards issues that might be important in the future, even though other equally relevant problems could have been proposed. No particular deadline for their solution is defined («millennium» refers to the start of the new millennium, it does not imply that they will be unsolved for a millennium). The most remarkable feature is that they spur scientific advancement; they are the type of problem that promotes the development of new theories, and therein lies their value.

«Topology is the branch of mathematics devoted to looking for the properties of spaces that can be used to determine their shape»

The Hodge conjecture is the fifth problem proposed by the Clay Mathematics Institute. The problem corresponds to the field of geometry (more precisely, in mathematical terms, to differential geometry and algebraic geometry). The problem was originally proposed by the Scottish mathematician William Hodge during the International Congress of Mathematicians, held in 1950 in Cambridge, Massachusetts, in the United States of America (Hodge, 1950). These conferences are held every four years and are the largest event in the field of mathematics. They bring different trends up to date with the most recent advances and the important Fields medals are awarded at them. Hodge was a plenary lecturer, and in his speech he presented the recent – at the time – theory of harmonic forms for the study of the topology of complex differentiable manifolds, known today as the Hodge theory. He also proposed extending a natural result of the representativeness of homology classes with submanifolds in differentiable manifolds to the case of complex manifolds.

(Left) Two spaces that can be obtained from each other with a reversible deformation and without breaking points apart are considered equal. In the picture, we observe the deformation of a doughnut into a teacup. Topologically, they are the same space. / Núria Server (Right) Each region of a surface can be drawn on a two-dimensional map with a grid. In the picture, a surface and its map. / V. Muñoz

The reader only has to count the number of words they find strange in the previous paragraph to realise the level of sophistication of current mathematics. Let us introduce those concepts now in order to make the formulation understandable.

Differential geometry

Geometry is the area of mathematics devoted to the study of geometric and physical spaces, and of figures (objects) and their interactions in such spaces. Geometry emerged in ancient Egypt and was further substantially developed in ancient Greece. Euclid’s geometry books are probably the most famous mathematical work in history. They describe the basic forms of planes and spaces (points, straight lines, polygons) and their interactions (movements and intersections). Later, geometry turned to curved forms (curves and surfaces) and developed in parallel to mathematical analysis. Isaac Newton created the concept of the derivative of a function to define the tangent vector of a curve. The most revolutionary concept appeared with the term differentiable manifold, which is the central object of differential geometry, and was introduced by Bernhard Riemann in the nineteenth century. A differentiable manifold is a space that locally (around any given point) appears to be a Euclidean space of a particular dimension n. Earth’s surface is a good example of dimension 2. Each region of a surface can be drawn on a two-dimensional map with a grid. A point on Earth corresponds to a position (x, y) on that map. Of course, these maps overlap, and the coordinates depend on the map, but we can traverse the entire surface if we have the complete atlas of all the maps that cover it.

«The Hodge conjecture corresponds to the fields of differential geometry and algebraic geometry»

The big step for geometry, already in the works for centuries and related to doubts regarding the inalterability of Euclid’s geometry postulates (which would end up leading to non-Euclidean geometries), meant realising that this local property does not force the entire space to be ℝⁿ. For non-mathematicians, ℝ is the straight line of real numbers (each position is marked by a real number), and ℝⁿ is the product of n real straight lines in n independent directions. Therefore, ℝ² is a plane (with two coordinate axes) and ℝ³ is the space (with three coordinate axes). Clearly, even though from Earth’s surface it looks like we are observing a plane around us, the Earth’s globe shape is not that of a plane. Our universe is the clearest example. It is a differentiable manifold of dimension 3 (here we omit time, and the notion of spacetime, in order to simplify our explanation). Locally, the universe can be mapped with three coordinates, but globally (in its entirety), it can have any shape we could imagine. Geometers have developed many ways to understand and «observe» spaces of three and more dimensions.

An important fact is that one can differentiate (find a derivative) on a differentiable manifold, and this allows us to note down any problem with intervening differential equations (like Newton’s gravitation theory or Einstein’s relativity theory). That is why we call it «differentiable».

Topology and homology

In order to classify manifolds, we need some mathematical properties to distinguish them. These are global properties (named so because manifolds are all the same locally, and can only differ globally). So, what makes a sphere and the surface of a doughnut – a torus in mathematics – different? First, we must carefully formalise the concept of «being different» and «being equal» (with mathematical terms such as «diffeomorphic»). Two spaces that can be obtained from each other with a reversible deformation and without tearing the space apart are considered equal. This occurs because both have equivalent atlases; that is, the same maps are valid for both, changing the scales of distances according to the deformations.

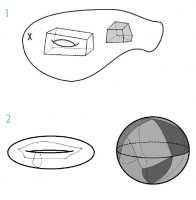
1) On the left, a hole of dimension k = 2 in a manifold X. On the right, an fictional hole. 2) On the left, 1-dimensional holes in a torus. On the right, a 2-dimensional hole of the sphere is surrounded by a curvilinear 2-polyhedron to cover the entire sphere.

The most noteworthy properties that have been used to distinguish differentiable manifolds are known as topological properties. Topology is the branch of mathematics devoted to looking for the properties of spaces that can be used to determine their shape. It is a relatively recent area, whose origins go back to Leonhard Euler, with his famous solution to the problem of the Königsberg bridges, but its official birth occurred in the twentieth century with Henri Poincaré. An important concept in topology is homology (Poincaré, 1895). The homology of a space counts the number of holes it has. A sphere and torus are different because they have a different number of holes (and, in fact, a different «type» of hole). Intuitively, a hole is «something missing» from a space, but the space is everything we have available and we cannot look for anything outside of it, because the space is nowhere in particular and there is nothing outside of it (think of our universe). The solution to the problem consists in looking for the hole in the space surrounding it with an object (a polyhedron is used by convention). In fact, a k-dimensional hole is defined as a polyhedron of dimension k, and the k-polyhedra that can be used as the border of a (k + 1)–dimensional polyhedron are eliminated, in which case there is actually no hole (it would be a fictional hole).

For example, in the case of the torus we have 1-dimensional holes given by polyhedra surrounding the torus in two directions. The sphere does not have these 1-dimensional holes, but it has a 2-dimensional hole that can be surrounded by covering the entire sphere. Those k-polyhedra are topological; that is, we should not consider them as straight lines.

«Hodge theory establishes a link between mathematical analysis and topology»

The holes can be added formally. To do so, we allocate coefficients to the faces of the polyhedra. The idea is that 2 times a cycle is equivalent to allocating it twice very closely together. But we could also consider allocating it a particular «weight». This weight (the coefficient allocated to the cycle) can be taken as a negative, a rational number such as 3/2, or even a real number. When we talk about homology with rational coefficients, we mean that we allow them to multiply the cycles by a rational coefficient.

A very important result by René Thom, which earned him the Fields Medal in 1958, states that any k-dimensional hole can be determined or «surrounded» by a k-dimensional manifold. A submanifold is a manifold within the ambient manifold X; for that to happen, its dimension k needs to be lower than the dimension n of X. Thom’s result has the peculiarity that it requires rational coefficients for its homology. Taking the case of a torus as an example, its 1-dimensional holes can occur for submanifolds of dimension 1; that is, for curves (instead of polygons).

Hodge theory

Hodge theory connects harmonic forms with homology elements, establishing a link between mathematical analysis and topology. To understand this, let us think about what happens to a unit of heat at a point in space. It dissipates and is distributed throughout space following what we call the heat equation, which has the following shape in three-dimensional space (t stands for the time and T for the temperature):

The final temperature distribution corresponds to the static case (when there is no heat transfer in the space), and is determined by the equation

or the so-called Laplacian equation (in honour of Pierre-Simon Laplace). Its solutions are called harmonic functions. For an n-dimensional space, more coordinates must be allocated. A similar process is behind the «dissipation» of k-submanifolds. To understand this, we need to exchange the functions with k-forms. A k-form is a mathematical object that can be integrated into a k-manifold, just as a function is evaluated at a point (note that a point is a 0-manifold). For example, the usual integral in ℝ³ is noted as ∫ f (x, y, z)dx dy dz, and the expression dx dy dz is an example of a 3-form.

«When we change the real numbers for complex numbers, many mathematical properties are simplified and become more uniform»

Hodge’s powerful theory states that any type of homology (in a closed, finite and borderless n-manifold) is given by a single harmonic form, following a dissipation process analogous to that of the heat equation. To do this, we need to use real coefficients in the homology. Therefore, the holes in a manifold are determined by solutions to a very special type of partial differential equation called elliptic equations, and which have many very useful analytical properties that are studied in depth in the field of partial differential equations.

During the International Congress of Mathematicians, held in 1950 in Cambridge, William Hodge presented the theory of harmonic forms for the study of the topology of complex differentiable manifolds, known today as Hodge theory. / John J. O’Connor & Edmund F. Robertson

Complex geometry

The next step of complexity in the abstraction leads us to use complex numbers (a redundancy in terms!). These numbers are noted as C and have the form z = x + iy, with x, y being real numbers and  being the imaginary unit. It is important to take into account that each complex number depends on two real numbers. All the squares of real numbers are positive, so the equation x² = –1 does not have a solution. The imaginary unit i is an artificially-added symbol that fulfils the property i² = –1. The general trend is that when we change the real numbers for complex numbers, many mathematical properties are simplified and become more uniform. Let us remember the fundamental theorem of algebra (shown by Carl Friedrich Gauss), which states that every polynomial equation has solutions in complex numbers, even if there are no solutions among real numbers (surprisingly, by adding the solution of an equation, all the polynomial equations then have solutions). In physics, introducing complex numbers is also common to understand real world processes, as in the study of electromagnetism. Geometry was not going to be any different. Thus, C² denotes the complex two-dimensional space, determined by two complex coordinates (z₁, z₂). Writing z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂, we deduce that each point in C² is determined by four real coordinates (x₁, y₁, x₂, y₂); that is, we are now in a real space of dimension 4. Similarly, C³ denotes the complex three-dimensional space, which has 6 real dimensions. In general, given a complex space E, the real dimension of E is twice its complex dimension. A complex manifold X is a differentiable manifold whose (local) coordinates are complex numbers. In complex manifolds, spatial intuition is lost because, with the change in dimensions, we cannot assimilate them to curves or surfaces in the real three-dimensional space.

The most studied complex manifolds are those that can be located in the C^N space given as the set of points where some polynomials vanish (more precisely, they are located in the complex projective space in order to obtain closed and borderless manifolds, but it is better not to incur into more technical terms here). These are called projective varieties and are the centre of attention in algebraic geometry. Because they are determined by polynomials, all the machinery of algebra can be used to obtain their properties (including their topological properties!). Indeed, the confluence of many ideas, theories, and arguments in this area is one of the characteristics that make mathematics beautiful.

«A conjecture is an open question that is believed to be true in some way, although we do not have a way to prove it»

Obtaining the conjugate is a basic operation with complex numbers. If z = x + iy, then its conjugate is z– = x − iy (only a sign changed). When considering differentiable forms in a complex manifold with (local) coordinates (z₁, z₂…, z_n), some depend on z variables (they are noted as dz₁, dz₂…, dz_n) and some depend on conjugated variables z– (noted as dz–₁, dz–₂…, dz–_n). However, there are also mixed variables which sometimes depend on one variable and in other cases on a conjugated variable (for instance: dz₁ dz–₂ dz–₃, which combines a complex term and two conjugates). In general, the forms are of the type (p, q), with p + q = k, containing p complex terms and q conjugated terms. For example, dz₁ dz–₂ dz–₃ is a (1,2)-form in a complex manifold of dimension 3 (and of real dimension 6, if the reader is not lost yet!). Solving the harmonic equation for the (p, q)-forms, gives us the harmonic (p, q)-forms and, as we have already indicated, also the homology elements of type (p, q); that is, the holes in the manifold that, because it is complex, have dimensions that are partly complex and partly conjugated (actually, it has p complex dimensions and q conjugated dimensions). Hence, we must use complex coefficients in homology (allowing the cycles to be multiplied by complex numbers). This has a very profound consequence that in a complex manifold each hole of a dimension k has a complex dimension p and a conjugated dimension q with k = p + q.

It can be proved that if a homology is represented by a complex submanifold of dimension p (and its real dimension is therefore 2p), then it is of the type (p, p). In other words, its complex and conjugated dimension compensate each other. Therefore, complex submanifolds represent holes (homology elements) that are rational (integers, in fact) and are of the type (p, p).

The importance of the problem

A conjecture is an open question that is believed to be true in some way, although we do not yet know a way to prove it. That is why counterexamples, the constructions that contradict a statement, are so impressive. However, Hodge did not raise the question as a conjecture, and there is no consensus on whether the conjecture is true or false. Opinions are very divided among the mathematicians who think we will be able to prove it and those who think it is false. The mathematician André Weil (1980) proposed a complex 4-fold as a possible counterexample, but it too has yet to be resolved. The Hodge conjecture stands out above other conjectures, such as the Riemann hypothesis (also included in the millennium problems), which everyone believes to be true.

Here, we outline a modern version that has already been simplified over time. It takes into account that slightly similar formulations have counterexamples (Grothendieck, 1969; Voisin, 2002). For instance, the version with integer coefficients is false (Atiyah & Hirzebruch, 1962). In any case, Hodge was not too precise in his question. He was merely trying to motivate research into Hodge theory and complex manifolds.

The conjecture is formulated as follows: If X is a projective manifold, any class of rational homology of type (p, p) can be represented by complex submanifolds of the complex dimension p. The formulation is proposed as an extension of Thom’s aforementioned result, where any class of rational homology of dimension k can be represented by a submanifold (a real one, which is understood when it is not specified) of dimension k. In this case, submanifolds are differentiable; that is to say, they are not necessarily given by polynomial equations.

«The importance of
a problem is shown
in the number of theories left along the way before it is solved»

The Hodge conjecture is difficult because complex submanifolds are very rigid objects (since they are defined by polynomials). In fact, it is very difficult to construct complex submanifolds, and there are very few of them. Proving that submanifolds exist without constructing them (a very helpful sort of indirect reasoning) has also been difficult. The fact that the problem belongs to a confluence area between algebraic geometry, differential geometry, and mathematical analysis – not to mention its connections to arithmetic geometry or to mathematical physics, which we have not discussed in here – turn this problem into an inexhaustible source of interactions. In fact, the importance of a problem is shown in the number of theories left along the way before it is solved. These theories will remain and open new lines of research, themselves useful for proposing new questions for the next millennium.