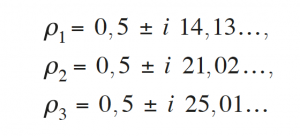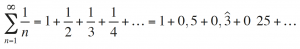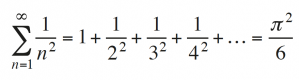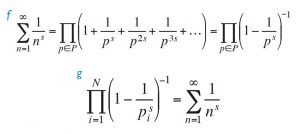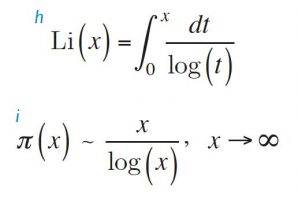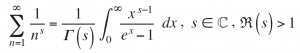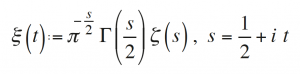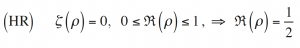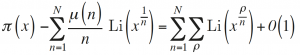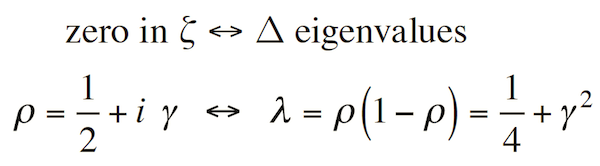The Riemann hypothesis

The Riemann hypothesis is an unproven statement referring to the zeros of the Riemann zeta function. Bernhard Riemann calculated the first six non-trivial zeros of the function and observed that they were all on the same straight line. In a report published in 1859, Riemann stated that this might very well be a general fact. The Riemann hypothesis claims that all non-trivial zeros of the zeta function are on the the line x = 1/2. The more than ten billion zeroes calculated to date, all of them lying on the critical line, coincide with Riemann’s suspicion, but no one has yet been able to prove that the zeta function does not have non-trivial zeroes outside of this line.

Keywords: prime numbers, zeta function, L-function, Riemann hypothesis, millennium problems.

Origin of the problem

The Riemann hypothesis is a still unproven statement referring to the function ζ(s), called the «Riemann zeta function». Proving that the zeta function is zero for negative even integers is not difficult: ζ(−2m) = 0, for m ≥ 1, which is why these numbers are called «trivial zeros». Bernhard Riemann (1826-1866) calculated another six zeros for the zeta function and observed that all their real parts are equal to 1/2:

In an 1859 report, Riemann said that this might be a general fact, although he did not know how to justify it. The Riemann hypothesis assumes that all non-trivial zeros of the zeta function lie on the line x = 1/2, called the «critical line».

The interest in locating the zeros of the Riemann zeta function was promoted by the German mathematician David Hilbert in 1900. It was the eighth item in his list of twenty-three open problems, which he presented to the International Congress of Mathematicians held in Paris at the beginning of the last century. Over the years, the involvement of the zeta function in many arithmetical problems has been highlighted, and proof of the Riemann hypothesis would imply the validity of many numerical results that depend on this statement. In particular, the zeta function is, by far, the most important analytical tool for studying prime numbers.

«The zeta function is, by far, the most important analytical tool for studying prime numbers»

With the help of computers, more than ten billion zeros of the zeta function have been calculated to date, all of them lying on the critical line, clearly highlighting Riemann’s extraordinary intuition. At the same time, extensive research on this issue – still insufficient to reach the final result – warns us of the enormous difficulty of the question, and when the Riemann hypothesis was included among the seven millennium problems, the Clay Institute reiterated the importance this hundred-year-old – yet still current – problem (Bombieri, 2000; Sarnak, 2005).

The harmonic series and prime numbers

To introduce the Riemann zeta function, it is useful to first consider the harmonic series, obtained by summing the inverse of all natural numbers:

The concepts of the arithmetic mean, geometric mean and harmonic mean of two numbers were already formulated by the Pythagoreans.

The harmonic mean h(a,b) of two numbers is defined as the inverse of the arithmetic mean of their inverses (a). The name harmonic series comes from the fact that each of its terms is the harmonic mean of the two neighbouring terms (b). The harmonic series is a divergent series; that is, the partial sums can be infinitely large. The medieval scholar Nicole Oresme (1323-1382) observed this and provided the following proof in the text Quaestiones super geometriam Euclidis (Oresme, 1961): it is clear that (c) and also that the selection of terms (d) are all larger than 1/2, and so on indefinitely; therefore (e).

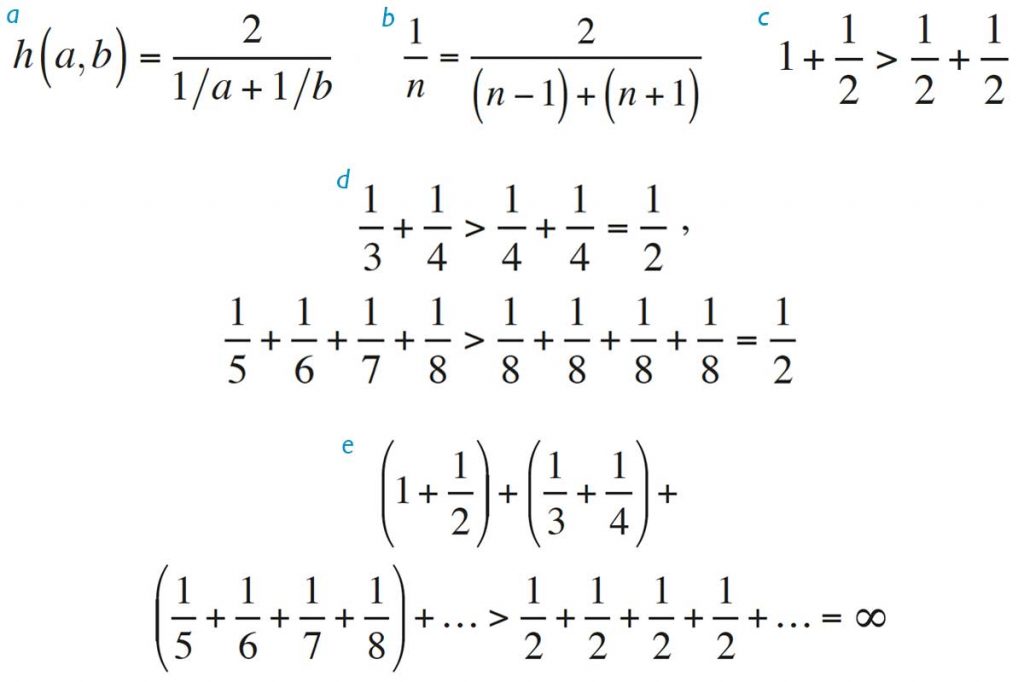
Later, the mathematician Pietro Mengoli (1626-1686), full professor of arithmetic of the University of Bologna, became interested in adding the inverses of the squares of all natural numbers, suspecting that this might be a convergent series, because it sums much smaller figures. Leonhard Euler (1707-1783) provided the exact value:

Replacing the exponent 2 in the series with any real number s, a convergent series is obtained for all values s > 1. This series was also evaluated by Euler for all positive even positive integers; in these numbers, the values of the zeta function are expressed as powers of π and depend on the so-called Bernoulli numbers, which are rational. From the outset, it was obvious that the series obtained in this way provided information about prime numbers and that its study led to a better understanding of what the Greeks had already learned about these numbers. From the sum of the geometric series 1/p^s, Euler obtained the infinite product (f) where the symbol P denotes the set of all prime numbers. Euler used the previous decomposition for the following proof, as an alternative to the one offered much earlier by Euclid, regarding the infinite nature of the set of all prime numbers. Let us assume that the set P = {p₁,…, p_N} is finite. This would give us (g).

However, for s = 1, the term on the left would represent a finite quantity, while the one on the right, as we have seen, would represent an infinite quantity. Using reductio ad absurdum, we can deduce that P is an infinite set.

In 1859, Bernhard Riemann (1826-1866) was elected member of the Academy of Sciences of Berlin. His admission monograph was devoted to the laws governing the distribution of prime numbers. In the picture, a portrait of the German mathematician. The Hilbert–Pólya conjecture gave rise to several physical and artistic interpretations of the Riemann hypothesis. On the left, the German mathematician David Hilbert (1862-1943). On the right, the Hungarian mathematician George Pólya (1887-1985). / Smithsonian Institution, Mètode

Euler – as anyone else could also realise – had already noted that prime numbers behave mysteriously: there is no formula to calculate the nth prime p_n directly and, should there be one, it would still be impossible to know the distance to the next prime p_n + 1 (Montgomery, 1973). This led to the first questions regarding the study of prime numbers being directed at obtaining formulae to provide an approximation to the number of primes π(x) below a given number when x tends to infinity. For instance, there are 25 prime numbers under one hundred, 168 under one thousand, 78,498 under one million, etc., but we do not have an explicit formula that can provide the exact value π(x) for any value of x.

After extensively studying prime number tables, Carl Friedrich Gauss (1777-1855) conjectured that π(x) ~ Li(x) when x → ∞, where the function (h) denotes the logarithm integral. The conjecture is equivalent to the asymptotic formula (i). The proof of this conjecture was the prime number theorem, first proved in 1896 by Jacques Hadamard (1865-1963) and Charles Jean de la Vallée-Poussin (1866-1962), independently from each other. However, it is worth noting the fundamental contribution that Riemann had already made to this field before this point.

The Riemann zeta function

In 1859, Riemann was elected as a member of the Academy of Sciences of Berlin. For his admission, he presented the study Über die Anzahl der Primzahlen unter einer gegebenen Grösse (“On the number of primes less than a given quantity”) (Riemann, 1859). The paper, whose manuscript did not exceed six pages, suggested that the laws governing the distribution of prime numbers largely depend on the behaviour of the harmonic series when it is extended to a complex variable function. Given a complex number s = x + iy, its real and imaginary parts are represented by R(s) = x and J(s) = y, respectively, and the entire set of complex numbers is represented by ℂ.

Consider the function of the complex variable defined by

In the formula, Γ(s) represents the gamma function that interpolates the factorial, another typically Eulerian creation. The previous series converges in the half-plane R(s) > 1, but the integral representation of the function it defines allows its analytical extension to the entire complex plane. The obtained function is the Riemann zeta function, ζ(s), which is only infinite at s = 1, where the harmonic series diverges. In fact, the behaviour of ζ(s) for R(s) < 0 is determined by the behaviour of ζ(s) for R(s) > 1. The values of ζ(s) that provide more information are located in the so-called critical strip, defined by 0 ≤ R(s) ≤ 1. The axis of symmetry of the critical strip is the straight line R(s) = 1/2, called the critical line. Evaluating the zeta function for negative integers, we obtain formulae equivalent to Euler’s and, particularly, we obtain the result that ζ(–2m) = 0, for every value of m ≥ 1; for this reason, even negative integers are called the trivial zeros of the zeta function.

Riemann stated that the zeta function has an infinite number of zeros on the critical strip, and offered an estimate of the number of zeros of bounded height. According to Riemann, we write:

The following comment about the zeros in ξ(t) can be found in Riemann (1859):

[…] it is very probable that all roots are real. Certainly one would wish for a stricter proof here; I have meanwhile temporarily put aside the search for this after some fleeting futile attempts, as it appears unnecessary for the next objective of my investigation.

The statement, according to which all non-trivial zeros of the Riemann zeta function are located in the critical line, is known as the Riemann hypothesis (RH):

Figure 1 represents the level curves of the zeros in the real (red) and imaginary (blue) sections of ζ(s). The zeros, represented with a black dot, are located in the intersections of the two curves. The two first trivial zeros and the first ten non-trivial zeros can be seen, as well as their symmetrical points, all of these on the critical line.

The central result obtained by Riemann in his paper was an asymptotic formula for calculating π (x) that connects the number of primes under a particular quantity with the zeros of the zeta function:

where μ(n) denotes the Möbius function, defined according to μ(n) = (–1)^k, if n is the product of k ≥ 0 different primes, and μ(n) = 0 otherwise.

Figure 1. The first zeros of the Riemann zeta function.

Riemann’s formula contains three types of terms: a) Terms that do not increase when x increases: included in 0(1); b) terms that increase when x increases: Li (x^1/n); and c) terms that increase in absolute value when x increases, oscillating in sign: Li (x^ρ/n). Riemann named these oscillatory terms «periodical», and his interpretation was that they are the cause of the experimentally observed fluctuations in the quantity of primes contained in each interval (Du Sautoy, 2003; Montgomery, 1973).

Riemann’s paper was, and still is, remarkably influential. Jacques Hadamard claimed to have needed three decades to understand its content and he proved all but one of Riemann’s statements: the Riemann hypothesis. In 1914, Godfrey Harold Hardy (1877-1947) proved that the function ξ(t) had an infinite number of real zeros; equivalently, the Riemann zeta function has infinite zeros in the critical line.

The Hilbert–Pólya conjecture

The so-called Hilbert–Pólya conjecture is based on a popular belief. It proposes a spectral interpretation of the non-trivial zeros of the Riemann zeta function; that is, there should be a linear operator, Δ, whose eigenvalues relate to the non-trivial zeros of the zeta function in the following way:

The Δ operator would be positive and written as Δ = D(1 – D), with i(D – 1/2) being a self-adjoint linear operator; therefore, the knowledge of such operators would allow us to state that their eigenvalues γ would be real numbers and the Riemann hypothesis would be proven.

It is commonly said that Hilbert called the set of eigenvalues of an operator the «spectrum», by analogy with the spectral lines produced by the radiation frequencies of atoms. Later, quantum mechanics would verify this interpretation: the spectral lines correspond to the eigenvectors of self-adjoint operators (which extend the properties of real symmetric matrices to the complex field), provided by the Hamiltonian of mechanical-quantum systems. Remember that Max Born (1882-1970), Werner Heisenberg (1901-1976), and John von Neumann (1903-1957) were Hilbert’s students in Göttingen.

The Hilbert–Pólya conjecture has given rise to several physical and artistic interpretations of the Riemann hypothesis. For instance, the fact that we can calculate the spectrum of an unknown operator has been compared to listening to music without knowing which instrument is playing it.

Proof of the Riemann hypothesis could also have consequences for other disciplines such as mathematical analysis or information theory. / Photo: Javier Quesada

Hasse–Weil zeta functions

The spectral interpretation of the zeros of the zeta function has also proven to be true in a very different context: for certain zeta functions arising from the study of polynomial equations. The zeta function of a complex variable, ζ(X,s) representing the number of points in the variety or the number of solutions of the system that defines it, can be associated to any projective and smooth algebraic variety X, defined over the finite field of q = p^f elements. The most important thing is that the points in these varieties can be interpreted as fixed points of an operator, which in this case is known, and is called Frobenius automorphism. The function is called the Hasse–Weil zeta function, and is much simpler than the Riemann zeta function. This is because it is a rational function in q^–s and its zeros – which are finite in number – satisfy an analogue of the Riemann hypothesis. The main contributions to this field were done by Emil Artin (1898-1962), Helmut Hasse (1898-1979), André Weil (1906-1998), Alexander Grothendieck (1928-2014), and Pierre Deligne, among many others. The Riemann hypothesis in the context of algebraic varieties over finite fields was proved by Deligne in the 1970s.

Afterword

The Riemann zeta function is a mathematical tool, created in the eighteenth and nineteenth centuries, in which complex variable analysis plays an important role. Riemann’s main goal was, in principle, to understand the behaviour of prime numbers. The Riemann zeta function is fundamental to understanding the distribution of these numbers, but we still lack a precise result regarding the position of the zeros of this function: i.e., the proof of the Riemann hypothesis. Proving it would imply having much more precise asymptotic rules in the field of analytical number theory; these laws are still currently only conjectures. Moreover, the proof of the Riemann hypothesis could also have consequences for other disciplines such as mathematical analysis or information theory. Thus, solving this problem would automatically imply solving many other related ones, which more than justifies the million-dollar reward!

During the nineteenth century we started to see that the model provided by the Riemann zeta function for the arithmetic study of integers could be extended to the arithmetic study of algebraic numbers; it was the birth of the Dedekind zeta function, the Dirichlet L-function and, in the twentieth century, the Artin L-function and the Hecke L-function. The twentieth century also witnessed the extension of the zeta functions and the L-functions to the study of varieties defined over finite fields, which we discussed above. But the story does not end here. The Riemann zeta function is the model for many other functions, also known as zeta functions or L-functions, the study of which defines a large part of the challenges proposed in twenty-first century mathematics.

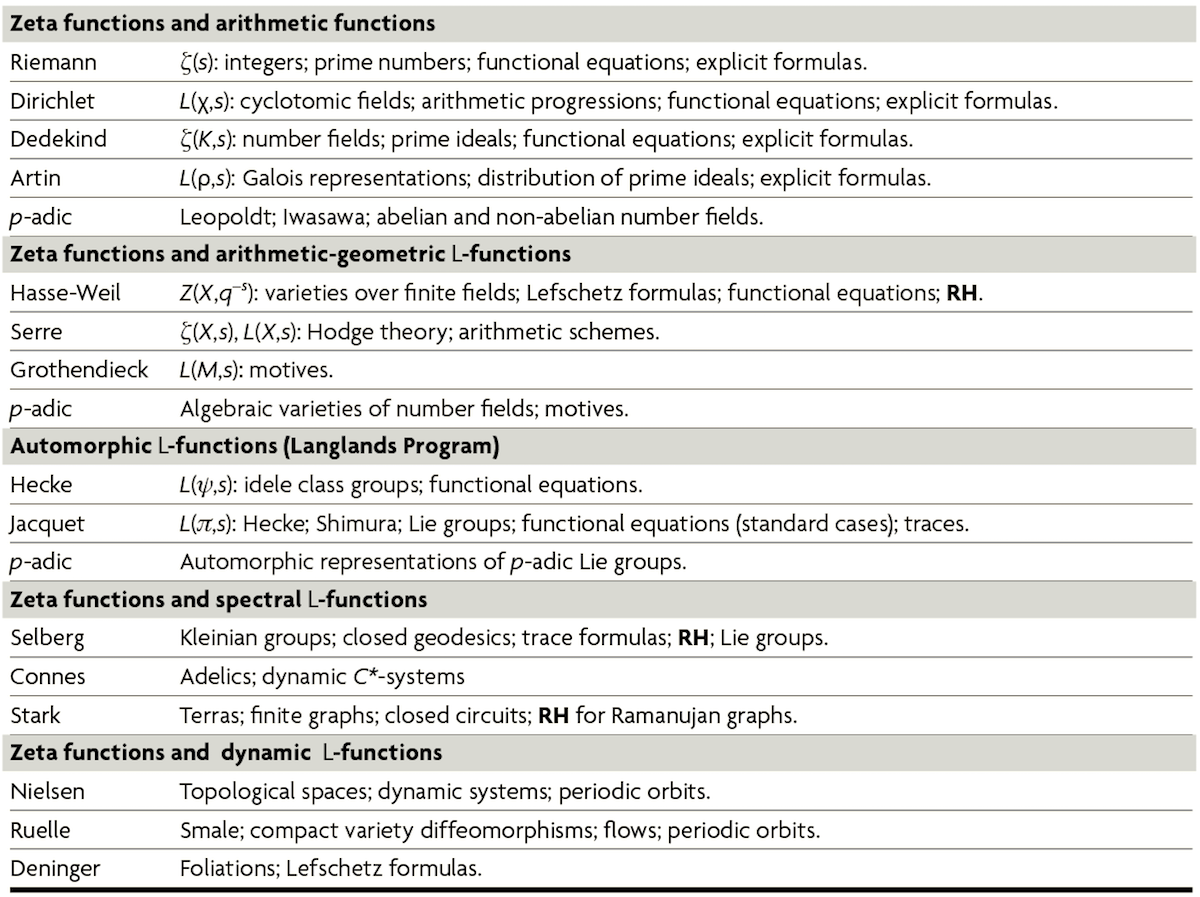
Table 1. A collection of zeta functions and L-functions, with their research area and most remarkable properties. The letters RH denote that a statement analogous to the Riemann hypothesis has been proved in the corresponding context. Source: Pilar Bayer, 2006. / Source: Pilar Bayer, 2006.

In Table 1 we offer a selection of mathematical objects with an associated zeta function or L-function. Some of the entries in Table 1 constitute fields and research programmes which are currently very large, such as the functions grouped under the name automorphic L-functions, which form the profound and extensive Langlands programme, offering a highly unifying vision of the Diophantine world. Readers who are interested in further information should check, among other citations, Bayer & Neukirch, 1978; Berry & Keating, 1999; Du Sautoy, 2003; Euler, 1737; Lagarias & Odlyzko, 1987; and Riemann, 1859, for the arithmetic case. For the arithmetic-geometric case, Deligne, 1974 and Weil, 1949; for spectral L-functions, Connes, 1999; Katz & Sarnak, 1999; Odlyzko, 2001; and Selberg, 1956, and for those related to dynamical systems, Deninger, 1998 and Lapidus & Van Frankenhuysen, 2001.

As we have seen, many mathematical objects have associated zeta functions. Given the amount of information they provide, we can interpret zeta functions, heterodoxically, as the DNA of these objects, given the amount of information they provide. We must, however, know how to extract and manage that information.