Illustration: Hugo Salais
When I was a child, my reference for a white-haired mad sage was Archimedes. My bedside book at the time, Dime quién es, told the story of his deranged and naked run shouting «Eureka!» all over Syracuse, after finding the solution to a problem that obsessed him: whether King Hiero’s crown was made of gold or the goldsmith had deceived him by gold-plating another metal. Perhaps out of childish decorum, the illustration showed him shortly before, in the bathtub, watching the water level rise after entering it. I also started to notice it when I bathed, without reaching the «Bingo!» moment, as my grandmother would put it. When I grew up and studied hydrostatics, the water level in the bathtub did not seem like a particularly cool observation. What did Archimedes really discover? And for what purpose?
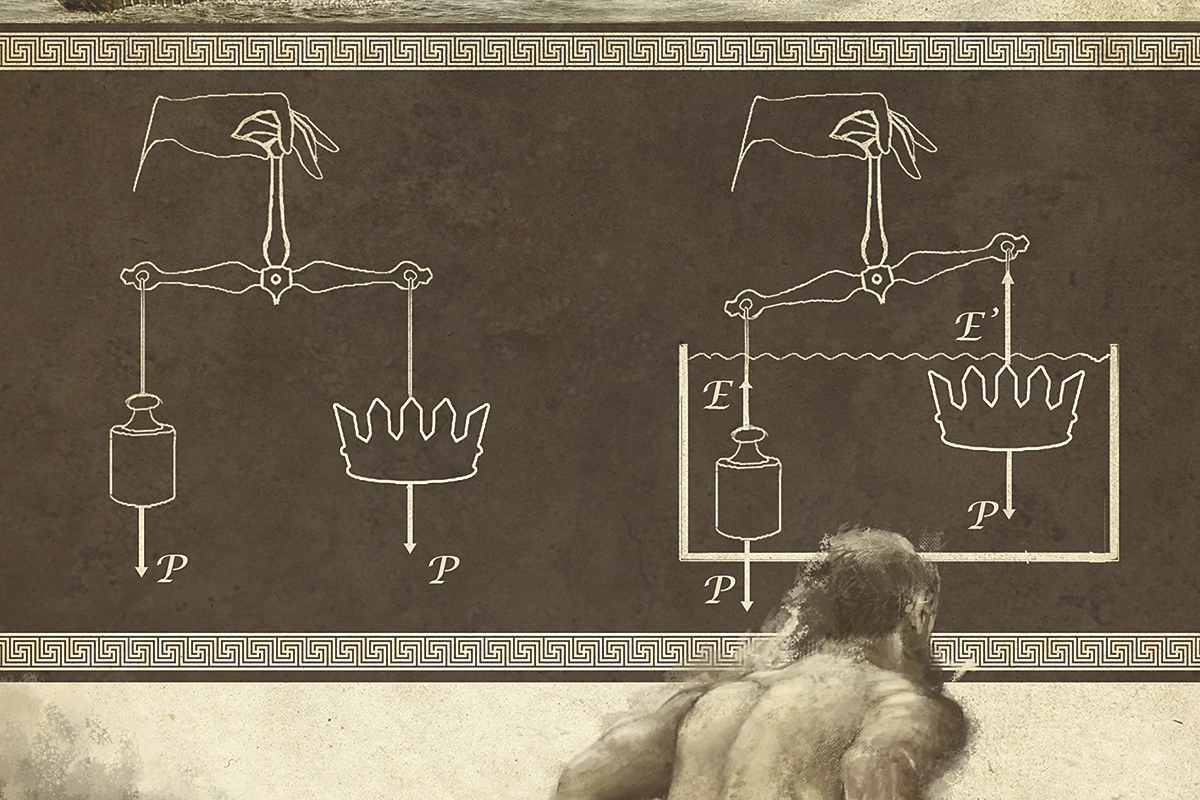
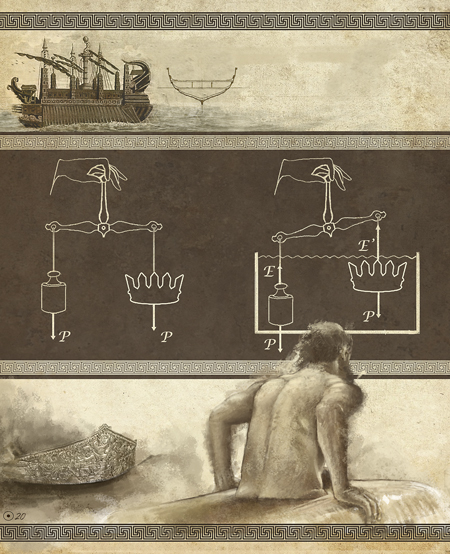
If we hold an object in our hand, we feel its contact force (equal to the weight of the object). Now we submerge both the hand and the object (it must not float) and notice that the contact force decreases. This is due to the appearance of the E force, which only depends on the mass of water displaced by the object when it is submerged and is due to the fact that the water pressure increases with depth. Given two identical balls, one made of lead and the other made of cork, totally immersed in water, the same force is felt. The weight of the cork ball is less than E, so when it is released, it rises and floats (and leaves a part of it out of the water). The weight of the lead ball is greater than E and the ball sinks. If I turn the lead ball into a hollow cup or bowl, the weight does not change, but now the thrust is greater: it displaces more water and it floats. On the other hand, and as the figure on the previous page illustrates, two bodies can have the same weight P and when introduced into a fluid, the balance is broken: this means that their volumes are different (different forces E and E’) and are made of different materials.
«The historian of science Alexander Koyrè summarised the scientific work of the sixteenth century as a gradual understanding of the works of Archimedes»
It is a well-known fact that Archimedes, like other Hellenistic scientists, tackled many physical and mathematical problems, and numerous technological projects, such as the manus ferrea (the Claw of Archimedes) that destroyed the Roman navy, the architronite – a steam cannon recovered by Leonardo da Vinci –, or the design of gears and pulleys, such as those used to launch the Syracusia, a kind of luxury Titanic with such a large hull to increase thrust that it could not anchor in nearly any port. He also supervised its construction and designed defensive deck catapults against piracy.
Galileo Galilei raged against Vitruvius (who originated the “eureka” legend) for trivialising the scientific sophistication of the man from Syracuse. In fact, the historian of science Alexander Koyrè summarised the scientific work of the sixteenth century as a gradual understanding of the works of Archimedes. Among them, the treatise “on floating bodies” that analyses the stability of bodies that have the shape of a bowl or paraboloid: the shape of any ship. Based on it, Galileo reconstructed the method for determining the density of a body, which is still used today. He would have liked the Archimedes painted by his contemporary José de Ribera, showing a Mediterranean skin, skinny and bald, with his mind entranced and a mischievous smile, thinking «Bingo!»
|
TRY IT: Try measuring the density of an object with your kitchen scale, for example a piece of plumbing or a key ring. It would be better if you can tie a string to it (I will use a bottle opener). Place a large glass of water on the scale and set it to 0 grams. Place the object on it (outside or inside the water, touching the base of the glass). Thus, the scale measures only the mass corresponding to the weight P of the object (I got mP = 73 g). Now suspend the object from the thread: holding one end of the thread, you submerge it completely, preventing the object from touching the bottom or the walls. In this case the scale measures the mass corresponding to the force E, that of the water that the object displaces when introduced (in my case, mE = 9 g). The relationship between the two masses mP/mE multiplied by the density of the water gives us the density of the object. In this case: (73/9) · (1 g/cm3) = 8,1 g/cm3. I looked up a table of densities online and discovered that the object must be made of copper or bronze (copper: approx. 8 g/cm3). |