The lack of reproducibility in research
How statistics can endorse results

|
Keywords: statistical evidence, hypothesis test, Bayesian analysis, uniformly most powerful Bayesian tests. Few rational people would accept the results of a scientific investigation if subsequent attempts to validate those results had already failed. So what would happen to the name of science if it was discovered that many respected studies’ findings were non-reproducible? We may be in the process of finding out. In a well-publicized coincidence, two pharmaceutical firms recently reported that they were only able to fully reproduce the peer-reviewed and published results of a small proportion of attempted studies: 20-25 % for one firm (Prinz, Schlange and Asadullah, 2011) and 11 % for the other (Begley and Ellis, 2012). Most of these studies tested investigational cancer treatments, where the failure rate of clinical trials is known to be high, but these findings are hardly unique. Researchers in other scientific fields have noted a shortfall in reproducible experimental results (see Hirschhorn, 2002, for example). We echo the sentiment expressed in another related article: «When seemingly implausible claims are made with conventional methods, it provides an ideal moment to reexamine these methods.» (Rouder and Morey, 2011). A good place to start such a reexamination is at conventional statistical methods. Although not well publicized outside of the statistical literature, there is a growing body of evidence suggesting that classical hypothesis tests, as they are typically used, are prone to overstating the strength of statistical trends. (Edwards et al., 1963; Berger and Sellke, 1987; Johnson, 2013a, 2013b). As a consequence, the very practices scientists use for analyzing their data are implicated as causes for the non-reproducibility of scientific research. Reaching wrong conclusions The problem associated with classical testing can be illustrated in a simple example. Imagine that disease W is known to kill 2 out of every 3 patients who contract it. Suppose that experimental drug A promises to improve the survival rate. If researchers perform a clinical trial, administering A to 16 patients, and 9 of these patients survive, then how does one conclude whether the drug was effective or not? If it was not effective, we would expect about one-third of 16, say 5, patients to survive. Is 9 patients «about» 5 patients? Or is it different enough from 5 to warrant a claim that the trial’s results are «significant», i.e. drug A is effective? The conventional method for answering this question is a one-sided hypothesis test, wherein we test a null hypothesis against its alternative. Let p denote the population survival rate after treatment with drug A, whatever it is. The null hypothesis (H0) states that p is less than or equal to 1/3, which means that the drug is ineffective. The alternative hypothesis (H1) states that p is greater than 1/3, which means that A helps, to some extent. In standard statistical practice, the null hypothesis is rejected in favor of the alternative hypothesis if the p-value of the experiment comes in below 0.05, where the p-value is defined as the probability, if H0 is true, of collecting data at least as extreme as the observed data. Thus, 0.05, which is known as the «size» of the test, is a threshold that divides those p-values that reject H0 from those that do not. In this drug trial, 9 out of 16 patients survived the disease after treatment with A. The p-value, the probability of observing 9 or more survivors out of 16 patients, if p is 1/3, can be calculated from simple probability theory. It turns out to be slightly less than 0.05. Thus, in a size 0.05 test we can reject the null hypothesis and conclude that the drug is effective. |
«So what would happen to the name of science if it was discovered that many respected studies’ findings were non-reproducible?» «Between 17% and 25% of all marginally significant findings in two psychology journals during 2007 were, in fact, false» |
|
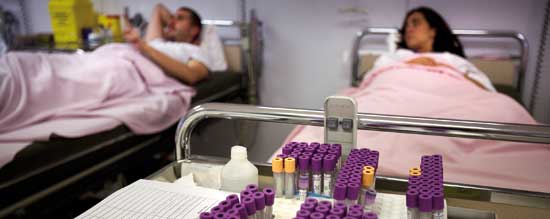 Edu Bayer/SINC Edu Bayer/SINCScience is based in the reproducibility of results. Two pharmaceutical firms recently reported that they were only able to fully reproduce the peer-reviewed and published results of less than 25% of their attempted studies. In the photograph, patients in a clinical trial. |
«The use of inadequate statistical methods can easily result in risky and wasteful outcomes» | |
|
The problem here, with regard to false discoveries and non-reproducibility, is that we are more likely to have made an incorrect conclusion than we may realize. Although some believe otherwise, a p-value of 0.05 does not mean that the probability that the null hypothesis is true is 0.05 (a nice discussion of this is found in Sellke, Bayarri and Berger, 2001). In fact, if we assume that the new drug was equally likely to be effective as ineffective then the probability in favor of null hypothesis is at least 0.15, which is distressingly high given that we just rejected it! This is the central problem of classical hypothesis testing: the p-value, when compared to a 0.05 threshold, may be small enough to reject the null hypothesis (meaning that the drug was ineffective), but it can still have a relatively high probability of being true. For scientists (indeed, for whole scientific disciplines) to continue using such a high threshold, while rarely reporting the probability that the null hypothesis is true, creates a breach in the defenses of statistical rigor that allows all kinds of erroneous claims to sneak into the hallowed realm of Scientific Fact. Actually, the 0.15 probability is a best-case scenario. Calculating the probability in favor of the null hypothesis is not a classical computation but rather a Bayesian one. Bayesian computations require additional assumptions, above and beyond those made in classical methods. These assumptions are called «prior» assumptions because they are made before any data are collected, like a preconceived notion that the experimenter carries into the research. In contrast, results that follow from data analysis are called «posterior» results; the value 0.15 is a posterior probability in favor of the null hypothesis. Calculating it requires the making of two prior assumptions. First, we must specify the prior probability that the null hypothesis is true, or our confidence in H0 before we recruit a single patient. Second, we must assume a value for p under the alternative hypothesis, since it is obviously higher than 1/3 if the drug is effective. Regarding the first assumption, here and throughout, we have simplified the exposition by assuming that the prior probability of H0 (and H1, for that matter) is 0.5. In the absence of any previous information about the new drug, this might well be a reasonable assumption. More troubling, though, is the question of what value p should be assumed to take, assuming that the alternative hypothesis is true (meaning in the example that the drug is effective). Differing assumptions regarding this probability lead to different posterior probabilities in favor of the opposite hypothesis, H0, and therefore to different conclusions. We calculated the value of 0.15 by assuming that if p is not 1/3, then it is 9/16. Of course, we could have set it anywhere between 0 and 1, but once the trial is conducted and 9 patients survive, a prior assumption that p = 9/16 turns out to be, of all the prior assumptions we could have made, the most hostile towards H0 (and yet recall that the resulting posterior probability of the null hypothesis, 0.15, was disheartening because it was not hostile enough). If we had instead assumed some other prior value of p, the posterior probability would be even higher than 0.15. For instance, for a prior assumption that p is either of 0.3618 or 0.75, the posterior probability of the null hypothesis rises to 0.39. There are three key takeaways from this example. First, it is evident that posterior probabilities frequently do not convey the same decisive indictment against the null hypothesis that classical p-values do. Second, posterior probabilities are highly dependent on the prior assumptions made concerning the parameter of interest under the alternative hypothesis, so that prior assumptions subjectively affect the outcome of the analysis. Third, the use of inadequate statistical methods can easily result in risky and wasteful outcomes, such as an ineffective cancer drug receiving scientific endorsement. Takeaways one and two are illustrated in a highly publicized investigation into extrasensory perception. Bem (2011) reports the results of nine experiments that test for the existence of the extrasensory perception, where the null hypothesis claims that it does not exist and the alternative hypothesis claims that it does. The author analyzed each experiment’s data by calculating classical p-values, and eight of the nine experiments yielded p-values less than 0.05. There were eight significant results in favor of extrasensory perception’s existence. Wagenmakers et al. (2011) criticized Bem for, among other things, relying on p-values, given their known tendency to exaggerate the weight of evidence against the null hypothesis, and provided a reanalysis of the data using Bayesian methods. They found posterior probabilities in favor of this hypothesis that claimed the no existence of extrasensory perception ranging between 0.15 and 0.88 for the nine experiments and concluded «the data of Bem do not support the hypothesis of precognition». In response, Bem, Utts and Johnson (2011) pointed out that the results of Wagenmakers et al. are highly sensitive to the prior assumptions made on the effect size under the alternative hypothesis. They further argued that those assumptions heavily weighted effect sizes that are not normally found in psychological experiments. Finally, they reanalyzed the data using the same Bayesian methods, but with «knowledge-based» prior assumptions under alternative hypothesis that put more weight on smaller effect sizes, and found posterior probabilities in favor of the null hypothesis ranging from 0.09 to 0.67, with most below 0.3. Uniformly most powerful Bayesian tests The hot debate over the methods used in Bem (2011) – which comprises many more articles than those here cited here – underscores the untrustworthy nature of p values and the controversy surrounding methods for calculating posterior probabilities. Depending on your opinion of extrasensory perception, it may also demonstrate how a misplaced trust in classical statistical hypothesis testing can award peer-reviewed approbation to a specious, unscientific claim. Recently, we proposed a new approach toward resolving the second of these problems, that of setting prior assumptions on p. The basic idea behind our proposal is that first, relevant stakeholders in the research should specify an evidence threshold for the posterior probability in favor of the null hypothesis, somewhat analogous to the threshold used on p-values. Following that, but before collecting data, researchers – who normally hope to reject H0 when the results come in – should be allowed to make the prior assumption under the alternative hypothesis that maximizes their chance of rejecting the null hypothesis. It turns out that this can be done in a relatively straightforward manner for a fairly broad class of tests. The resulting tests are called uniformly most powerful Bayesian tests, and we can illustrate their use in the context of our hypothetical drug trial. |
«A misplaced trust in classical statistical hypothesis testing can award peer-reviewed approbation to a specious, unscientific claim» |
|
 CERN CERNThe probability in favor of the Higgs boson particle’s existence may be in the neighborhood of 0.999963 to 0.999977. Strong evidence, but perhaps not quite as strong as that implied by the original report. In the photograph, the physicists François Englert and Peter Higgs, during the announcement of the discovery in the CERN. |
||
|
Suppose the clinical trial’s sponsor demands, for example, that the null hypothesis only be rejected if its posterior probability falls below 0.05. For an experimenter who wants to declare the new drug a success, the relevant question in setting p under the alternative hypothesis then becomes, «What assumed value of p will maximize the probability that the posterior probability in favor of H0 will fall below 0.05?» Using methodology in Johnson (2013a), the most favorable prior assumption that the investigator can make is p = 0.63. This value maximizes the probability that the posterior probability of the null hypothesis will fall below 0.05, regardless of the true value of p. From the investigator’s perspective, this is the optimal choice of all possible assumptions under the alternative hypothesis, and if we allow investigators to make this choice, the subjectivity in selecting the alternative hypothesis is eliminated. Incidentally, using a prior survival probability under the alternative hypothesis of p = 0.63 and a threshold of 0.05 means that the null hypothesis will only be rejected if 11 or more patients survive after receiving drug A. This is the same criterion that would be used to reject the null hypothesis in a classical test of size 0.004. Hence, requiring the posterior probability for the null hypothesis to fall beneath a low threshold (0.05) for significance implies that the p-value must fall beneath a very low threshold (0.004). In this case, uniformly most powerful Bayesian tests have simultaneously provided an objective way to make prior assumptions under H1 and curtailed the excessive permissiveness of classical hypothesis tests. Furthermore, because uniformly most powerful Bayesian tests can be used to specify objective prior assumptions under the alternative hypothesis, they are useful for going back and computing posterior probabilities in publications where classical p-values were originally reported. Using these methods, Johnson (2013a) argues that the posterior probability in favor of the Higgs boson particle’s existence may be in the neighborhood of 0.999963 to 0.999977 – strong evidence, but perhaps not quite as strong as that implied by the reported p-value of 3×10-7. In another article (2013b), he uses these tests to estimate that between 17% and 25% of all marginally significant findings in two psychology journals during 2007 are, in fact, false discoveries. Finally, returning to the study on extrasensory perception, we can use an approximate version of the uniformly most powerful Bayesian test to obtain posterior probabilities for the null hypothesis between 0.12 and 0.39, when 0.05 is used as the threshold for significance. Conclusion In summary, we wish to emphasize that currently used thresholds in classical test of statistical significance are responsible for much of the non-reproducibility of scientific studies that has been noted in the popular press and in subject matter journals. Among the thousands of claims made in publications every year, a large fraction of those which are marginally significant at the 0.05 level are, in fact, false discoveries. However, Bayesian testing methods that calculate the posterior probability in favor of the null hypothesis alleviate the unreliability of p-values, and when prior assumptions under the alternative hypothesis are made using uniformly most powerful Bayesian tests, the resulting posterior probability is both objective and equivalent to a classical test, but with higher standards of evidence. We view these Bayesian testing methods as a simple and potent way to reduce the non-reproducibility in modern science. |
«Bayesian testing methods are a simple and potent way to reduce the non-reproducibility in modern science» |
|
REFERENCES
Begley, C. and L. Ellis, 2012. «Drug Development: Raise Standards for Preclinical Cancer Research». Nature, 483(7391): 531-533. doi: 10.1038/483531a
Bem, D., 2011. «Feeling the Future: Experimental Evidence for Anomalous Retroactive Influences on Cognition and Effect». Journal Personality and Social Psychology, 100(3): 407-425. doi: 10.1037/a0021524
Bem, D.; Utts, J. and W. Johnson, 2011. «Must Psychologists Change the Way they Analyze Their Data?». Journal Personality and Social Psychology, 101(4): 716-719. doi: 10.1037/a0024777
Berger, J. and T. Sellke, 1987. «Testing a Point Null Hypothesis: Irreconcilability of p-values and Evidence». Journal of the American Statistical Association, 82(397): 112-122. doi: 10.2307/2289131
Edwards, W.; Lindman, H. and L. Savage, 1963. «Bayesian Statistical Inference for Psychological Research». Psychological Review, 70(3): 193-242. doi: 10.1037/h0044139
Hirschhorn, J.; Lohmueller, K.; Byrne, E. and K. Hirschhorn, 2002. «A Comprehensive Review of Genetic Association Studies». Genetics in Medicine, 4(2): 45-61. doi: 10.1097/00125817-200203000-00002
Johnson, V. E., 2013a. «Uniformly Most Powerful Bayesian Test». The Annals of Statistics, 41(1): 1716-1741. doi: 10.1214/13-AOS1123
Johnson, V. E., 2013b. «Revised Standards for Statistical Evidence». PNAS, 110(48): 19313-19317. doi: 10.1073/pnas.1313476110
Prinz, F.; Schlange, T. and K. Asadullah, 2011. «Believe It or Not: How Much Can We Rely on Published Data on Potential Drug Targets?». Nature Reviews Drug Discovery, 10(9): 712. doi: 10.1038/nrd3439-c1
Rouder, J. and R. Morey, 2011. «A Bayes Factor Meta-analysis of Bem's ESP Claim». Psychonomic Bulleton and Review, 18(4): 682-689. doi: 10.3758/s13423-011-0088-7
Sellke, T.; Bayarri, M. and J. Berger, 2001. «Calibration of p-values for Testing Precise Null Hypotheses». The American Statistician, 55(1): 62-71. doi: 10.1198/000313001300339950
Wagenmakers, E.; Wetzels, R.; Borsboom, D. and H. van der Maas, 2011. «Why Psychologists Must Change the Way they Analyze Their Data: the Case of Psi: Comment on Bem (2011)». Journal of Personality and Social Psychology, 100(3): 426-432. doi: 10.1037/a0022790
 The central problem of classical hypothesis testing is that the p-value may be small enough to reject the null hypothesis but it can still have a relatively high probability of being true. This allows all kinds of errors such as an ineffective cancer drug receiving scientific endorsement.
The central problem of classical hypothesis testing is that the p-value may be small enough to reject the null hypothesis but it can still have a relatively high probability of being true. This allows all kinds of errors such as an ineffective cancer drug receiving scientific endorsement.