Illustration: Hugo Salais
In one of those family table talks where you learn about your family history, my father told me that when he was a child and lived in our home town, he used to play with a sling. From the point of view of my urban childhood, with no fast-running lizards, reed flutes, or climbing trees, I imagined David’s pinpoint shot – more divine than human – to bring Goliath down. Quite recently I learned that in this case reality surpasses the myth: no one aimed better and had more deadly power than a Balearic slinger. They appear in many classical sources. Balearic slingers fought the Greeks during the Sicilian (580–265 BC) and the Punic wars (264–146 BC). Hannibal considered his two thousand slingers irreplaceable and placed them in the front lines to break enemy defenses. Later, as Roman auxiliary troops, the funditores (the name comes from the term funda, sling) fought alongside Julius Caesar both in Gaul and in Britain.
Probably of Paleolithic origin and present since the first civilisations, the sling is ancient and ubiquitous not only as a weapon, but also as the paradigm of circular movement, in which direction changes continuously while its value remains constant. As the reader can see in both the illustration and the engraving – extracted from Descartes’s Principia philosophiae – the object or projectile in the sling moves in a circle along points ABF … L. Without the thread tension, it would follow a straight line (points ACG). That tension represents a force towards the centre of the circle that continually deflects it (an equal and opposing force to that which operates on the hand). What happens when the slinger releases the shot or the sling breaks (at A, for instance)? The thread tension disappears and the projectile goes away following the ACG tangent at the speed it had before detaching from the sling.
«The sling is ancient and ubiquitous not only as a weapon, but also as the paradigm of circular movement»
Unless other forces affect them, objects move in a straight line at a constant speed. If the movement is circular, there must be a force pushing towards the centre of the circle: a vehicle can run along a curved road thanks to the lateral friction on the tyres on the ground (what happens if there is ice on the road?). The contact of the washing machine drum with the rest of the structure makes the clothes spin (but not water, which goes out in a straight line through the holes). Electrons circulate through the synchrotron ring thanks to magnetic force (there are magnets, what happens if we turn them off?). Our Moon orbits the Earth thanks to our gravitational pull (which cannot be removed from the equation). The same occurs with the Earth around the Sun and with our Sun around the centre of our galaxy.
Kepler, Galileo, or Newton might have remembered their childhood sling when they read Plutarch’s (first century AD) De facie quae in orbe lunae apparet: «Therefore the moon is not drawn down by her weight, since that tendency is counteracted by her circular movement. (…) For everything is borne on in its own natural direction
unless this is changed by some other force.» And maybe Anaxagoras (sixth century BC), to whom Plutarch attributes this idea, formulated it thinking of a Balearic slinger. Not just the Moon or a sling go around in circles.
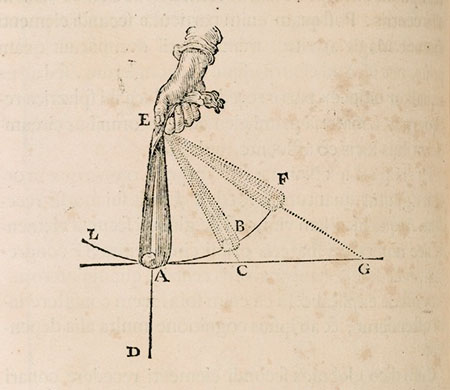 Engraving from Descartes’s Principia philosophiae depicting the circular motion of a sling. / Mètode TRY IT: Try to make a sling with whatever you have at hand: a keychain tied with a thread, a potato in a scarf, etc. Spin it over your head (be careful!) with constant speed and keeping the sling in a horizontal position. You will feel the tension in your hand, with the same force as the spinning object, but in the opposite direction. Observe: the time that it takes the object to complete a turn (period t) increases as you let go of more thread (r). Using your phone’s stopwatch (or a video), you can count up to ten turns to obtain t. My sling, for r = 20 cm, took 4.9 seconds to complete 10 rotations (t = 0.49 s). When r = 80 cm, the time doubles (t = 0.98 s). This means that r / t2 (related to tension and centripetal acceleration) is constant at 0.8 for both. |