When the state of the art is ahead of the state of understanding

Deep learning is an undeniably hot topic, not only within both academia and industry, but also among society and the media. The reasons for the advent of its popularity are manifold: unprecedented availability of data and computing power, some innovative methodologies, minor but significant technical tricks, etc. However, interestingly, the current success and practice of deep learning seems to be uncorrelated with its theoretical, more formal understanding. And with that, deep learning’s state-of-the-art presents a number of unintuitive properties or situations. In this note, I highlight some of these unintuitive properties, trying to show relevant recent work, and expose the need to get insight into them, either by formal or more empirical means.

Keywords: deep learning, machine learning, neural networks, unintuitive properties.

Introduction

In the last years, neural networks have resurfaced from their ashes, yielding impressive outcomes in tasks where traditional approaches were systematically underperforming (LeCun, Bengio, & Hinton, 2015). The reasons for this success are manifold, and they are still a matter of debate. Clearly, there are data and technological components that have decisively contributed, namely the availability of unprecedented volumes of data and the ubiquitous access to greater computing power. However, besides those more practical components, I would say it is safe to claim that one of the key enablers of the current success of neural networks has been the introduction of minor but significant «tricks of the trade». Some examples were the initialization of the neurons’ weights by unsupervised pre-training, the substitution of sigmoid activations by rectified linear units to alleviate the problem of vanishing gradients, or the systematic and extensive use of convolutional architectures to tackle translations while reducing the number of trainable weights.

«In the last years, neural networks have resurfaced from their ashes, yielding impressive outcomes»

Interestingly, a majority of these enabler tricks do not stem from a unified theory of neural networks nor from rigorous mathematical developments. Instead, they stem from intuition, empirical investigation and, ultimately, trial and error (or brute-force search). In this sense, deep learning research seems to follow Wolfram’s «new kind of science» paradigm (Wolfram, 2002), under which «the optimal design of [deep learning] systems can only be approached by a combinatorial search over the vast number of all possible [network] configurations». In fact, some researchers have directly embraced this mantra and started the search, with the help of automatic and/or structured methodologies to partially guide it. For example, Zoph and Le (2016) discover novel network configurations using evolutionary strategies.

But the empirically-driven advancement of the field should not prevent the development of more formal theories (or proto-theories) that would allow us to comprehend what is going on and, eventually, provide a more holistic understanding of it. In particular, such understanding could take ground from a number of open issues or unintuitive properties of neural networks that puzzle the research community (Larochelle, 2017). In the remaining of the article, I will present and try to briefly explain some of these unintuitive properties.

Neural networks can make dumb errors

It is now well known that neural networks can produce totally unexpected outputs from inputs with perceptually-irrelevant changes, which are commonly called adversarial examples. Humans can also be confused by «adversarial examples»: we all have seen images that we guessed were something (or a part of something) and later we were told they were not. However, the point here is that human adversarial examples do not correspond to those of neural networks because, in the latter case, they can be perceptually the same. Szegedy et al. (2014) showed that a network could misclassify an image by just applying «a certain hardly perceptible perturbation» to it. Not only that, but they also found that the same perturbation on that particular image caused misclassification even when the image was not in the training set, that is, when the network was trained with a different subset of images. Complementarily, Nguyen, Yosinski, and Clune (2015) showed that it is possible to produce artificial images that are completely unrecognizable by humans but that, nonetheless, deep neural networks believe to be real-world recognizable objects with a 99.99% confidence.

The problem of adversarial examples is interesting because they contradict one of the most renowned and extensively demonstrated qualities of neural networks: their large generalization capability (or, in other words, their outstanding performance on unseen data). Knowledge on possible adversarial attacks is increasing (Papernot et al., 2017), and with it, new techniques to tackle the problem appear. Incipient theories have arised, and recent work suggests that adversarial examples are directly related to model performance (Gilmer et al., 2018). However, to day, a general understanding of the phenomenon is missing.

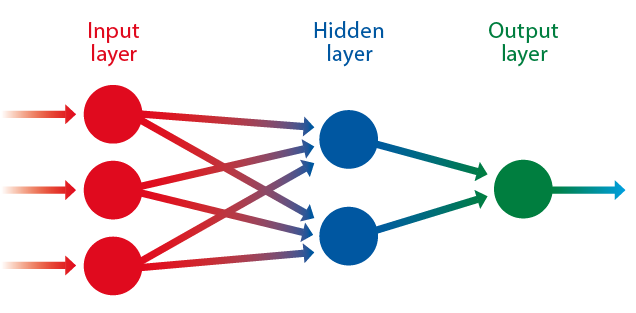
Artificial neural networks are modelled after the neural system of a biological brain. Each node in the structure represents one of the neurons located at different levels (input, hidden, and output layers) processing the «training» data in the deep learning process. / Adapted from Wikipedia

The solution space is a mystery

As with many other machine learning algorithms, the training of neural networks proceeds by finding a combination of numbers, called network parameters or weights, that yields the highest performance or, more properly, the minimum loss on some data. If we had only a single weight, training the network would consist in finding the value of that weight which results in the minimum loss of information. There are well known methodologies to find such a minimum for a few parameters with theoretical guarantees. However, deep neural networks are typically in the range of millions of parameters, for which a suitable combination that minimizes a certain loss must be found. The number of parameters per se would not be a serious problem if the loss was convex, that is, that it had a single minimum and that, roughly speaking, all strictly descending paths reached that minimum. However, this is not the case. The losses of current deep networks are non-convex, with multiple local minima.
In this scenario, there are not many theoretical guarantees about the ability of most known methodologies to find a good minimum (ideally the smallest minimum over all minima). In general, the loss landscapes induced by deep networks are totally unknown, and the explored fraction of the solution space is tiny. Apart from multiple local minima, loss landscapes are supposed to include saddle points (Dauphin et al., 2014) and other obstacles that theoretically hinder the «navigation» of current minimum-finding algorithms. Nonetheless, extremely basic minimum-finding algorithms reach good solutions; as good as to break the state-of-the-art in well-studied problems, and as to tackle newly proposed, previously unthinkable machine learning tasks. Why is that?

«It is interesting that a research field like deep learning can present so many breakthroughs and, at the same time, so many puzzling situations»

A common hypothesis is that the vast majority of local minima are almost of a similar loss, that is, all of them imply equally good solutions (Kawaguchi, 2016). Another hypothesis is that saddle points and other obstacles are not encountered during minimum search with current methods (Goodfellow, Vinyals, & Saxe, 2015). It is also very possible that some architectures or design priors introduce convexity (Li, Xu, Taylor, & Goldstein, 2017). All these could explain why random weight initializations, together with the simplest minimum-finding algorithms, actually work. In fact, such algorithms seem to perform best when badly conditioned, or when some noise is introduced in the process.

Neural networks can easily memorize

Even a not-so-deep neural network belongs to the class of what is called universal function approximation algorithms (Cybenko, 1989). That means, in plain words, that neural networks have enough power to represent any data set. Recent work empirically shows that finite-sized networks can model any finite-sized data set, even if this is made of shuffled data, random data, or random labels (Zhang, Hardt, Recht, & Vinyals, 2017). This has the implication that neural networks can remember the labels of any training data, no matter the nature of that data. And remembering training data means performing with 100% accuracy on such data.
What is not so obvious is that, still, if the data is not totally random, neural networks are totally capable of extrapolating their memories to unseen cases and generalize. Doing so when the number of model parameters is several orders of magnitude larger than the number of training instances is what is intriguing and not yet formally justified. It contradicts the classical machine learning rule of thumb to prefer simple models (in the sense of having few learnable parameters) in order to achieve good generalization capabilities. It also contradicts conventional wisdom that some more or less explicit form of irrelevant parameter pruning, commonly called regularization, should be employed when a model is much bigger than the number of training instances (Zhang et al., 2017).

Neural networks can be compressed

Parameter pruning or explicit regularization is not needed for generalization. However, it is well known that one can drastically reduce the number of parameters of a trained neural network and still maintain its performance on both seen and unseen data (Han, Mao, & Dally, 2016). Even ensembles of neural networks can be «distilled» into a smaller network without a noticeable performance drop (Hinton, Vinyals, & Dean, 2014). In some cases, the amount of pruning or compression is surprising: up to 100 times depending on the data set and network architecture.

«Even if the data is not totally random, neural networks are capable of extrapolating their memories to unseen cases and generalize»

The possibility of severely compressing neural networks has obvious practical consequences, specially when such networks need to be deployed in low-resource devices, like mobile phones, or limited-hardware systems, like cars. But besides practical considerations, it also poses several questions: do we need a large network in the first place? Is there some architecture twist that combined with current minimum-finding algorithms allows to discover good parameter combinations for those small networks? Or is it just a matter of discovering new minimum-finding algorithms?

Learning is influenced by initialization and example order

As with human learning, current network learning depends on the order in which we present the examples. Practitioners know that different sample orderings yield different performances and, in particular, that early examples have more influence on the final accuracy (Erhan et al., 2010). Furthermore, it is now a classic trick to pre-train a neural network in an unsupervised way or to transfer knowledge from a related task to benefit from additional sources (Yosinski, Clune, Bengio, & Lipson, 2014). In addition, it is easy to show that even though random initializations of the networks’ weights converge to a good solution, changing the initial weights’ distributions or the distributions’ parameters can affect the final accuracy or, in the worst case, just prevent the network to learn at all (LeCun, Bottou, Orr, & Müller, 2002). There is a lack of knowledge on mathematically-motivated initialization schemes, as well as on optimal orderings of training samples. A general theory seems difficult to find and, as the variety of neural network architectures grows every day, individual, mathematically-motivated policies struggle to catch up.

Both artificial neural networks and the human mind can be confused by «adversarial examples», images we identify as something (or as a part of something) and are later found to be something else. However, an artificial network can misclassify an image just by applying some barely perceptible disturbance. In the picture, a collage inspired by the meme «chihuahua or muffin?» which gained popularity in 2016 as an example of the potential confusions affecting artificial intelligence neural networks. / Mètode

Neural networks forget what they learn

In stark contrast to humans, neural networks forget what they learn. This phenomenon is known as catastrophic forgetting or catastrophic interference, and has been studied since the beginning of the nineties (McCloskey & Cohen, 1989). Essentially, when a neural network that has been trained for a certain task is reused for learning a new task, it completely forgets how to perform the former. Beyond the relatively philosophical objective of mimicking human learning and whereas machines should be able to do so or not, the problem of catastrophic forgetting has important consequences for the current development of systems that consider a large number of (potentially multimodal) tasks, and for those which aim towards a more general concept of intelligence. As for now, it looks unrealistic that such systems may be able to learn from all possible relevant data at once, or in a parallel fashion.
With years, there have been various attempts to overcome catastrophic forgetting. Some of the most common strategies include the use of memories, rehearsal or «dreaming» parallels, attention strategies, or constraining the plasticity of neurons (Serrà, Surís, Miron, & Karatzoglou, 2018). In a more general vein, the problem of catastrophic forgetting may stem from the backpropagation algorithm itself, which represents the very essence of modern neural network training. Perhaps an elegant solution to the issue requires of a major rethinking of the current paradigm.

Conclusion

It is interesting that a research field like deep learning, which drives such an enormous amount of attention (from academia to industry or the media), can present so many breakthroughs and, at the same time, so many puzzling situations. The state of the art may be quite ahead of the state of understanding, and this situation may continue like that for years. Nonetheless, it could also well be that even a minor theoretical advancement forces a paradigm shift that later fosters a more formal and mathematically-grounded approach to deep learning. Until then, empirical exploration will continue to be the major way through, and the main tool to bridge the gap between practice and understanding, remembering of the new kind of science approach.