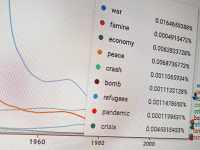
Architecture and Mathematics
Geometry at the service of art: from Gaudí to Gehry
|
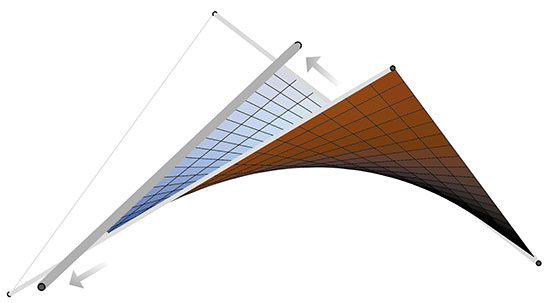
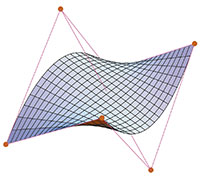
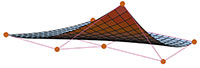
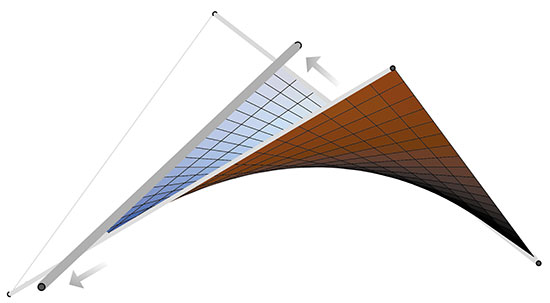
Architecture and Mathematics, Geometry and Art: from Gaudí to Gehry. No one is surprised by the fact that mathematics has a direct application in architecture. Every one of us can imagine that, before getting down to work, architects have to verify that the structure they want to build is achievable given the strength of the materials to be used, the loads they have to endure and perhaps also the economic cost. However it seems that this application is reduced only to this, the calculation of stabilities, stress, etc., but in no way to the design of the architectural object itself. We think, and it is true, that with regard to artistic creation, architects push mathematics out of their desks and let their imagination run free in pursuit of the desired shape. Well, this is not exactly true. What many people may not know is that mathematics can also help, and in fact they do, not in the magical moment of artistic creation itself but in the immediately following stage. «All architectural creation is geometry» is a maxim that can be found in the treaties of descriptive geometry. Architects have always used surfaces that can be described as classic, which they combined rightly. And today, they continue to do so. A new theory, the one formulated by Bézier on surfaces and their generalisations, which originated in the early 60s in various automotive and aircraft construction companies, can help architects design surfaces at random with simplicity and elegance. Let me try to explain how architecture has been nourished in the last century not only by mathematical techniques, but also by its ideas. We will take a tour from Gaudí’s Sagrada Familia to Gehry’s Guggenheim, exploring also the work of the Mexican Félix Candela and the Olympic stadium in Munich. A journey that will bring us from the classic surfaces used in architecture to the modern computer-generated surfaces. Geometry and architecture before the computer One of the most implemented surfaces in architecture is the one that receives the pompous name of hyperbolic paraboloid. Gaudí was one of those who used it, but Félix Candela is the one that worked with it the most. Within the fauna of the surfaces, the hyperbolic paraboloid is a specimen that was already known to the Greeks. Conic curves (the ellipse, the parabola and the hyperbola) are for two-dimensional space the same quadric surfaces are for three-dimensional space. The names of these surfaces are related to the curves appearing as sections with planes. In the hyperbolic paraboloid, one of the quadric surfaces, these sections are parabolas and hyperbolas. But the really important property, which sparked the interest of both Gaudí and Candela, is the fact that the hyperbolic paraboloid, despite being a curved surface, can be constructed with straight lines. All one has to do is to vary the angle of inclination of a line that moves above another curve. Geometers call these surfaces ruled surfaces and we can find many examples in other art, in sculpture. Presumably this is the property that allowed Gaudí to give precise instructions to his workers and to his foreman when they had to build a hyperbolic paraboloid on the roof of the Sagrada Familia (begun 1883). Let’s see exactly how to construct one. Given four points in space that are not in the same plane, there is a single hyperbolic paraboloid that crosses these four points. This is the same property that says that two points determine a single line. The task of the workers was to join with a bar each of the pair of points of a side, and the opposite pair with another bar. Then we just have to let another bar slide on the previous two maintaining a constant speed at the ends. Gaudí used the hyperbolic paraboloid and also other doubly ruled surfaces as the hyperboloid of revolution. The one who showed a sublime mastery in its use was the architect of Spanish origin, exiled to Mexico and then an American citizen, Félix Candela. The best example can be found in Los Manantiales Restaurant (1958) at Xochimilco Park in Mexico City. The roof consists of eight hyperbolic paraboloids. The same structure can be found now in the new Oceanogràfic (2002) of the City of Arts and Sciences of Valencia. The Oceanogràfic, photographed during construction, showing its structure. Both Gaudí and Candela took advantage of previously defined and studied mathematical surfaces, with perfectly determined equations and a fully established way to construct them. This implies a lack of freedom in the design of the desired shape. They could only use a certain family of surfaces depending on a few parameters. The only variation allowed is to play with different parameter values. The genius of the two architects and the experience gained after many tests with models made it possible to overcome this defect. Representation as a union of parts of a hyperbolic paraboloid of the roof of the Oceanogràfic’s hall. MINIMAL SURFACES IN ARCHITECTURE The following example of using a particular type of surface in architecture can be found in two of the buildings of the Olympic complex in Munich (1972). The roof of the Olympic Stadium and of the pool are examples of those minimal surfaces. Known to geometry since the seventeenth century, these surfaces have the property of being, among all those that share the same border, those with minimum area. The property of minimising is the one used by German architect Frei Otto to erect, through a system of supports and cables, a surprisingly lightweight structure which nullified inner tension, allowing to reduce materials and to use bold forms. Minimal surfaces, despite allowing more degrees of freedom than the exclusive use of the hyperbolic paraboloids, still have restrictions. These restrictions basically appear due to the fact that, because of the border, minimal surface is fully determined. Therefore, designers of surfaces can only act on the border and hope that the resulting minimum surface presents the desired shape. This problem, the lack of freedom in design, which appears with the use of quadric or minimal surfaces, was also raised in the beginning of a new discipline: to obtain curves and surfaces of different shapes but with a simple procedure. This cannot be achieved with equations, since intuition, unfortunately for geometers, is lost when we replace a surface by an equation. We need a simple geometric procedure to construct complicated shapes. This was the idea at the design centre of the Citroën car company when, in the close of the ’50s, they hired a young mathematician. In the words of the mathematician himself, «neither he knew what to do in that company, or, what is worse, nor did the company know what to do with a mathematician». The fact is that they posed him a problem related to design and the answer he gave is now known as the beginning of computer-aided geometric design. His surname was DeCasteljau, but the curves and surfaces he devised are now known by the name of Bézier curves and surfaces, in honour of another mathematician who, independently and alternatively, came to the same solution while working for a competitor, Renault. The explanation for this change of name is both simple and cruel: Citröen’s intellectual property policy was much more restrictive with their workers than Renault’s. DeCasteljau was not allowed to publish his work in scientific journals, with everything that the international dissemination of results entails, which Bézier was instead able to do. DeCasteljau’s idea for constructing surfaces has its roots in the hyperbolic paraboloid itself. We have already seen that a hyperbolic paraboloid is determined by four points. Somehow we can say that these points control the surface. The idea is to use a network of points that control the surface, and construct the surface with a procedure similar to that used by construction workers, which in mathematics is known as linear interpolation, recursively. It should be noted that one of the key ingredients that computer experts and mathematicians exploit when designing an algorithm is recursion. Therefore, DeCasteljau’s construction is fully adapted to the new working tool that the computer represented in the early years of its appearance. CAGD IN ARCHITECTURE In Les Alqueries, La Plana Baixa, we could see in early summer of 2002 a structure being erected at the side of the road that was quite a striking sight. It was the wooden frames that would support the roof of a new restaurant. The building is rectangular, without any ornament in its walls, very classical. However, the most striking feature is the shape of the roof. In contrast to the use of straight lines and completely flat walls, the roof almost flew with is gracefully curved structure. Almost as if a magic flying carpet had been placed as a roof. The glass walls emphasise this feeling. Now, the roof is none other than one of the simplest surfaces of the new discipline. The roof that could be seen in early summer of 2002, fully finished in early fall, is the example of the most simple Bézier surface, apart from the hyperbolic paraboloid. It is still a ruled surface. Two sides of the surface are parabolas, one concave and the other convex. The other two are line segments. We can think of the surface as a family of line segments, supported at their ends on both parables. That is, Gaudí’s workers would have let the bar slide with the ends on the two parabolas. This area still retains one of the properties of the hyperbolic paraboloid, it is still a ruled surface. The dimensions of the control net are 3×2. An example of a Bézier surface with a higher degree of complexity can be constructed with a control net of 3×3. Well, it turns out that we can find an architectural materialisation in the city of Valencia, particularly in the north end of the Malvarrosa beach. We do not have to travel very far to find the most emblematic application of computer-aided architectural design, the Guggenheim Museum (1997) by Canadian architect Frank O. Gehry. Its curved edges, the sinuous shape of the titanium-coated walls, the multiform volumes, irregular geometry, in short, are the product of the will to integrate the building into the surrounding environment and of the support that its creator has found in design software based on the concepts of Bézier curves and surfaces and their generalisations. The embryo of the Museum’s design is a few scribbles. Only with additional information can we relate the sketch to the final result. Despite this, the creative spark is there. Everything that comes after is art. However, the notion of Bézier surfaces helped the architect to easily go from the Muses to the paper. In the words of the architect himself: «…Next, the computer makes the models and I use them as a final visual review. Then, with the computer… I think the equation between architect and construction changes». We can imagine the architecture office with the architect working with a computer-aided design software (this one was called CATIA, developed by a French aerospace company) doing tests after tests, relocating the control points, until the screen showed what he had in mind. If you ever visit the museum in Bilbao, remember that its cover, the building, both the exterior and the interior, is also a work of art of an architect of his time, an electronic Vitruvius, who took advantage of mathematical tools in the process of creation. Tools that allowed his sculptural visions to transform into a workable project. |

Photography of Los Manantiales restaurant in Mexico City. Explicit description of part of the hyperbolic paraboloid used by architect Félix Candela. «All architectural creation is geometry» Photos (above) of the restaurant in Les Alqueries under construction, where you can see the structure, and of the restaurant already finished. Below, representation as Bézier surface of the roof of this restaurant in Les Alqueries. Above, photo of a bar in the Malva-Rosa, Valencia. «In the words of the mathematician himself, ‘neither he knew what to do in that company, or, what is worse, nor did the company know what to do with a mathematician’» Photos of the roof of the Cabanyal station in Valencia. Photos of the Guggenheim Museum in Bilbao, by Canadian architect Frank O. Gehry. |