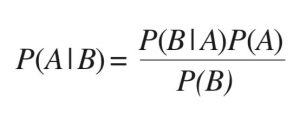The theory that never died

Bayes’s rule, a simple eighteenth century theory about assessing knowledge, was controversial during most of the twentieth century but used secretly by Great Britain and the United States during World War II and the Cold War. Palomares and Valencia played important roles in its development in those dark days. The rule is widely used today in the computerized world and in many applications. For instance, Bayes has become political shorthand for something different: for data-based decision-making. The Bayesian Revolution turned out to be a modern paradigm shift for a very pragmatic age.

Keywords: Bayes’s rule, Fisher, frequentists, Laplace.

A simple mathematical theory discovered by two British clergymen (Bayes, 1763) in the eighteenth century has recently taken the modern computer-driven world by storm. In fact, it is such a pervasive part of our computer-driven lives today that it has become chic – even politically correct – in some prominent quarters of the United States.

Yet, during most of the twentieth century, it was so controversial that many people who used it did not dare mention its name. During the most beleagued period of Bayes’s history, two places in Spain – Palomares and Valencia – played vital roles in keeping the theory alive.

The theory is almost ludicrously simple. It helps people evaluate their initial ideas, update and modify them with new information, and make better decisions. In brief, Bayes’s rule is a simple one-liner: Initial Beliefs + Recent Objective Data = A New and Improved Belief.

As the prominent British economist, John Maynard Keynes, said sarcastically, «When the facts change, I change my opinion. What do you do, sir?»

During the eighteenth century, two clergymen and amateur mathematicians, an Englishman, Thomas Bayes, and his Welsh friend, Richard Price, discovered and published the theorem, and French mathematician Pierre-Simon Laplace developed it into the form used today. Now, we would call it the Bayes-Price-Laplace theory or BPL for short.

The theory is remarkably powerful. In practice, Bayes requires multiple calculations, and powerful computers re-integrate the probability of an initial belief millions of times as each new piece of information arrives. Bayes does not produce an exact, absolutely certain answer. Instead, using probability, it inches toward the most probable conclusion. Nevertheless, thanks to Bayes, we can filter spam, assess medical and other risks, search the Internet for the web pages we want, and learn what we might like to buy, based on what we’ve looked at in the past. The military uses it to sharpen the images produced when drones fly overhead, and doctors use it to clarify our MRI and Pet Scan images. It’s used on Wall Street and in astronomy and physics, the machine translation of foreign languages, genetics, and bioinformatics. The list goes on and on.

«A simple mathematical theory discovered by two British clergymen in the eighteenth century has recently taken
the modern computer-driven world by storm»

Here’s Exhibit A of the power of Bayes today: finding things lost at sea. During the Cold War, the United States Air Force lost a hydrogen bomb off the coast of Palomares, and the U. S. Navy started secretly developing Bayesian theory to find objects underwater. In 2009, Air France Flight 447 disappeared with 228 people aboard into the South Atlantic Ocean. By then, the U.S. Navy had developed Bayesian search theory enough so that it ended a fruitless, two-year search for AF447’s wreckage after one-week of undersea searching. Bayesian search experts hope the theory can also help find the lost Malaysian Flight 370.

In Exhibit B of Bayes’s power, Google’s driverless car starts out with detailed information from maps of route and road conditions. As the car drives through traffic, sensors on top of the vehicle gather new traffic data to update the initial information and calculate what is probably the safest way to drive at that particular moment.

Exhibit C of the power of Bayes today involves spam filters. Many people, including myself, can remember beginning work each morning by wading through Viagra ads. Mercifully, that changed when a patent for Bayesian spam filters was issued to Microsoft in 2000.

Benjamin West. Portrait of Richard Price, 1784. Oil on canvas, 87.5 × 185 cm. Price was convinced that the theorem would help to prove the existence of «God The Cause». After two years editing Bayes’s theorem, he published it in an English journal. / Llyfrgell Genedlaethol Cymru, The National Library of Wales

Enlightenment

But to understand why such a useful theory would have caused an uproar during much of the twentieth century, we have to go back to the beginning, to the Reverends Thomas Bayes and Richard Price, during the 1740s. An inflammatory religious controversy was raging over the improbability of Christian miracles. At issue was the question whether evidence about the natural world could help us make rational conclusions about God the creator, what the eighteenth century called The Cause or The First Cause.

We do not know that Bayes wanted to prove the existence of God the Cause. But we do know that he tried to deal mathematically with the problem of cause and effect. However, Bayes did not believe in his theorem enough to publish it. He filed it away in a notebook until he died 10 or 15 years later. In his will, he gave 100 pounds to Price with a request: to please look through his unpublished papers.

Going through them, Price decided boldly that the theorem would help prove the existence of God the Cause. After two years spent editing Bayes’s theorem, he got it published in an English journal that, unfortunately, few mathematicians read.

A few years later, in 1774, a great French mathematician, Pierre Simon Laplace, discovered the rule independently of Bayes and Price. Laplace named it the Probability of Causes. Unlike Bayes and Price, Laplace was the quintessential professional scientist. He mathematized every science known to his era and spent 40 years on and off developing what we call Bayes’s rule (Laplace, 1812). In fact, until about 50 years ago, Bayes’s rule was known as Laplace’s work. By rights, it should still be called Laplace’s rule.

After Laplace’s death in 1827, a very different attitude about assessing scientific evidence took hold of the statistical world. Over the course of the 1700s and early 1800s, Western scientists, governments, instrument makers, and clubs of amateurs worked hard accumulating lots of precise and trustworthy data. Some of their famous data collections measured the chest sizes of Scottish soldiers, the number of Prussian officers killed by kicking horses, and the incidence of cholera victims.

The Anti-Bayes reaction

With lots of precise and trustworthy numbers at their disposal, up-to-date statisticians rejected Bayes’s rule and preferred to judge the probability of an event according to how frequently it occurred. Eventually, they became known as frequentists. Until a few years ago, they would be the great opponents of Bayes’s rule.

For the frequentists, modern science required both objectivity and precise answers. Measuring anyone’s initial and subjective belief and computing probabilities and approximations seemed like «subjectivity run amok», «an aberration of the intellect» and «ignorance […] coined into science». By 1920, most scientists thought Bayes «smacked of astrology, of alchemy», and a leading statistician said Bayes’s formula was used «with a sigh, as the only thing available under the circumstances».

«Bayes did not believe in his theorem enough to publish it. He filed it away in a notebook until he died ten or fifteen years later»

The surprising thing is that all this time – as theorists and philosophers denounced Bayes’s rule as abhorrently subjective – people who had to deal with real-world emergencies and make one-time decisions based on incomplete information continued using Bayes’s rule. For them, Bayes helped them make do with what they had.

Thus, for example, Bayes’s rule helped free Dreyfus from a French prison for treason in the 1890s. Artillery officers in France, Russia and the US used it to aim their fire and test their ammunition and cannons during two World Wars. Insurance and telephone company executives in the United States also used Bayes during the First World War.

Now every good story needs a villain, and the villain of our piece is a great statistician: Ronald Aylmer Fisher of Cambridge University. During the 1920s and 1930s, quantum mechanics unleashed a cultural reaction against probability and uncertainty, and statistical theoreticians like Fisher changed their attitudes about Bayes from tepid toleration to outright hostility.

Jean-Baptiste Guérin Paulin. Pierre-Simon marquis de Laplace (1745-1827), 1838. Oil on panel, 146 × 113 cm. In 1774, the French mathematician Pierre Simon Laplace discovered the rule independently of Bayes and Price. Laplace named it the Probability of Causes. / Grand Palais (Château de Versailles)

Fisher’s attacks were especially important because he was a giant in statistics when it was still in its infancy (Fisher, 1925). He also had an explosive temper. He called it «the bane of my existence». A colleague called Fisher a «contentious, polemical man. His life was a sequence of scientific fights, often several at a time, at scientific meetings and in scientific papers». He even interpreted scientific questions as personal attacks. And he hated Bayes’s rule.

Fisher didn’t need Bayes. Bayes is especially useful when data is sparse and uncertain, and Fisher had data about precisely how much fertilizer had been applied to various farm plots. He filled his house with cats, dogs, and thousands of mice for breeding experiments and, as a fervent eugenicist and geneticist, he could document each animal’s pedigree for generations. His experiments were repeatable and they produced precise answers. He called Bayes «a mistake (perhaps the only mistake to which the mathematical world has so deeply committed itself) […] founded on an error and [the rule] must be wholly rejected». After another Cambridge scientist and statistician, Harold Jeffreys, used Bayes to trace tsunamis back to the earthquakes that had caused them, Fisher said Jeffreys’s book on probability (Jeffreys, 1931) had made a «logical mistake on the first page which invalidates all the 395 formulae in his book». The mistake, of course, was using Bayes’s rule (Aldrich, 2004, 2008).

Second World War era

Hence, at the start of World War II in 1939, Bayes was almost taboo among statistical sophisticates. Fortunately for Britain and the United States, Alan Turing was not a statistician. He was a mathematician. Needing to make emergency decisions based on scanty evidence, Turing used Bayes extensively; first, to crack the German Enigma codes ordering U-boats around the North Atlantic, and second, to build the Colossi computers designed to crack other German codes during the war.

«During the 1990s new computational methods, and free software finally allowed Bayesians to calculate realistic problems with ease»

After the European peace, however, the British government classified as a state secret everything showing that mathematics, statistics, decoding, computers and Alan Turing had helped win the war. The edict may have prevented Britain from becoming the leader of the twentieth century computer revolution. It certainly prevented mathematicians and statisticians from becoming war heroes.

With its wartime successes totally classified, Bayes’s rule emerged from World War II even more suspect than before. After Jack Good, Turing’s wartime statistical assistant, discussed Bayesian theory and methods at the Royal Statistical Society, the next speaker’s opening words were: «After that nonsense…». Harvard Business School professors who developed Bayesian decision trees were called «socialists and so-called scientists». When Hans Buehlmann, the future president of ETH Zurich, visited Berkeley’s very frequentist statistics department in the 1950s, he realized «it was kind of dangerous» to defend Bayes. So he used Bayes but invented different, neutral terminology which, he thought, protected the Continent from much of the Anglo-American contempt for Bayes.

During the Cold War, the United States Air Force lost a hydrogen bomb off the coast of Palomares, and the U. S. Navy started secretly developing Bayesian theory to find objects underwater. In the picture, the shell of two B28 nuclear bombs from the Palomares incident, as shown in the National Museum of Nuclear Science & History, in Albuquerque, NM. / Plumbob78

Ironically, as Bayes became taboo, the U.S. military continued to use it in secret. For example, a classified study at the Rand Corporation in California used Bayes to warn that expanding the U.S. Air Force’s practice of flying jets armed with hydrogen bombs around the world could produce many more accidents like the one at Palomares. The Kennedy administration eventually added safeguards. The U.S. Navy used it to find Soviet submarines in the Mediterranean. In 1973, the first safety study of the U.S. nuclear power industry relied on Bayesian methods and predicted what happened during the 1979 accident at Three Mile Island in Pennsylvania.

Revival and the proof of its worth

Not knowing Bayes’s success stories, a small group of maybe 100 or more believers struggled for acceptance during the Cold War. Many Bayesians of that generation remember the exact moment when Bayes’s overarching logic suddenly converted them like an epiphany. For them, Bayes’s rule had what Einstein called «the cosmic religious feeling».

The battle between the Bayesians and anti-Bayesian statisticians became so vitriolic and personal that, when an American Bayesian took his 9-year-old son to a party in mid-1960s, a guest told the little child «that his father was a deeply deluded man».

Left: The military use Bayes’s rule to sharpen the images produced when drones fly overhead. / Don McCullough. // Right: Google’s driverless car starts out with detailed information from maps of route and road conditions. As the car drives through traffic, sensors on top of the vehicle gather new traffic data to update the initial information and calculate what is probably the safest way to drive at that particular moment. / Steve Jurvetson

During this distressing period, José M. Bernardo, a statistics professor at the University of Valencia, used then radically new Bayesian methods for political analyses. He conducted a Bayesian analysis of political polling for the Socialist party in 1982 during the elections that won power for the Socialist party under Felipe González. Bayes is good for updating hypotheses with a variety of data, including the probability of voter trends and attitudes. Later, Bernardo became a scientific adviser to the government during Gonzalez’s presidency and conducted other Bayesian applications for it. In the meantime, Bernardo also played an important role for Bayesian camaraderie. He convinced the first (centrist) democratic government after the fascist dictatorship that financing an international conference for Bayesian statisticians in 1979 would help publicize the emergence of democratic Spain. That endeavor was so successful that the State of Valencia financed a second and third conference. After that, no subsidies were needed because it was considered a privilege to be invited and statisticians could easily get travel money from their home institutions. Other funds provided grants to new Ph.Ds. The meetings, held every four years, were vital to Bayesians for developing a sense of solidarity, reviving spirits, and discussing the latest theories and methods. Over the years, the conferences grew from roughly 100 attendees to so many that the conference had to be moved to increasingly bigger facilities. Now an international organization of Bayesians (ISBA), it continues the conference every two years: in Kyoto, Japan, in 2012 and in Cancun, Mexico, in 2014.

During the 1990s the outlook changed radically for Bayes. Powerful desktop computers, new computational methods, and free software finally allowed Bayesians to calculate realistic problems with ease. Outsiders from computer science, physics and artificial intelligence poured into the field, refreshing, broadening, depoliticizing, and secularizing it. After 250 years of fits and starts, it was adopted almost overnight.

Alan Turing used Bayes extensively, first, to crack the German Enigma codes ordering U-boats around the North Atlantic, and second, to build the Colossi computers designed to crack other German codes during the war. In the picture, a statue of the mathematician in Bletchley Park Museum. / Duane Wessels (Bletchley Park Museum)

During the past few years, Bayes has suddenly become something that many trendy Americans think they should know something about. For example, when Alan B. Krueger became chair of President Obama’s Council of Economic Advisers, he made a completely gratuitous plug to my book about Bayes (McGrayne, 2013) in the New York Times: «I recently finished reading McGrayne’s book […] Bayes’s rule is a statistical theory that has a long and interesting history. It is important in decision making – how tightly should you hold on to your view and how much should you update your view based on the new information that’s coming in. We … [and remember he’s the President’s adviser] intuitively use Bayes’s rule every day».

So, suddenly in our dogmatic era, when many leaders are proud to make decisions based on dogma they received as children, Bayes has become political shorthand for something different: for data-based decision-making. In a remarkable development, Bayesian statistics – once the province of clergymen and 100 embattled Cold War believers – has become part of the White House’s vocabulary.

The Bayesian Revolution turned out to be a modern paradigm shift for a very pragmatic age. It happened overnight – not because people changed their minds about Bayes as a philosophy of science –
but because suddenly Bayes worked.